Binomial, ein Programm zur Binomialverteilung
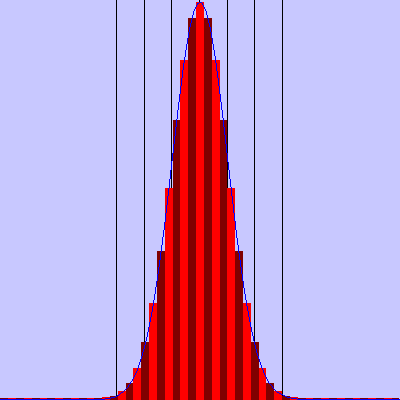
- Zeichne das Histogramm der Wahrscheinlichkeitsverteilung oder die kumulierte Verteilung. Berechne beide Verteilungen zu gegebener Anzahl k der Erfolge. Variiere den Stichprobenumfang n und die Erfolgswahrscheinlichkeit p. Speichere das Diagramm als *.png.
- Veranschauliche σ-Umgebungen durch die Striche (grau) und durch die Anzeige von k und z. Reskaliere das Diagramm so, dass die Konvergenz für n → ∞ deutlich wird. Zeichne die entsprechende Kurve der Gaussschen Normalverteilung (blau).
- Berechne Konfidenzintervalle oder Verwerfungsbereiche zu gegebenem Signifikanzniveau α.
- Arbeitsblätter mit Erklärungen und Aufgaben sind ins Programm integriert. (Der Text ist auch unten zu finden.)
Download 5.0 MB
Integrierte Erklärungen und Arbeitsblätter:
Mehr lesen ...
Wieder verstecken ...
Es gibt (103) = 120 Möglichkeiten, an welcher Stelle eine Sechs auftritt (Pfade im Baumdiagramm), und jeweils die Pfadwahrscheinlichkeit (1/6)3*(5/6)7 = 0,001292045 , also ist die Wahrscheinlichkeit 120 * 0,001292045 = 0,155045 .
Binomialverteilung: Allgemein betrachten wir einen n-stufigen Versuch, wobei auf jeder Stufe der "Erfolg" mit derselben Wahrscheinlichkeit p eintritt. Die Wahrscheinlichkeit, dass die Anzahl X der Erfolge einen Wert k hat, ist dann P(X = k) = (nk)pkqn-k mit q = 1 - p . Der Binomialkoeffizient (nk) läßt sich z.B. mit dem Pascalschen Dreieck berechnen, oder auf vielen Taschenrechnern mit der Taste "nCr".
Das Programm Binomial zeigt die Binomialverteilung durch ein Histogramm an. Mit den Tasten p und n kannst Du die Erfolgswahrscheinlichkeit p und den Stichprobenumfang n verändern. Mit der Taste x kannst Du einen Wert für k eingegeben und die Wahrscheinlichkeit P(X = k) berechnen.
Die kumulierte Wahrscheinlichkeit ist die Wahrscheinlichkeit für höchstens k Erfolge,
P(X ≤ k) = P(X = 0) + P(X = 1) + ... + P(X = k) .
Das Programm berechnet mit der Taste x auch die kumulierte Wahrscheinlichkeit. Für spezielle Werte von p und n gibt es auch Tabellen, und eine allgemeine Näherungsformel wird auf Seite 5 vorgestellt. Die Berechnung mit dem Taschenrechner wäre für große k sehr mühsam. Mit der Taste F2 wird die kumulierte Verteilung als Diagramm dargestellt, und zwar als Integralfunktion des Histogramms. Jeweils der rechte Rand eines Trapezes gibt eine kumulierte Wahrscheinlichkeit an.
Beispiel 2: Für n = 100 und p = 0,4 ergibt sich die Wahrscheinlichkeit für mindestens 30 und höchstens 40 Erfolge,
P(30 ≤ X ≤ 40) = P(X ≤ 40) - P(X ≤ 29) = 0,543294 - 0,014775 = 0,528519 .
Aufgabe 1: Berechne die Wahrscheinlichkeit mit dem Taschenrechner und mit dem Programm:
Bei n = 37 und p = 0,58 ist P(X = 25) = ? Lösung 1.
Aufgabe 2: Bestimme die kumulierte Wahrscheinlichkeit mit einer Tabelle und mit dem Programm:
Bei n = 50 und p = 1/6 = 0,16666667 ist P(X ≥ 10) = ? Lösung 2.
Aufgabe 3: Berechne die kumulierte Wahrscheinlichkeit mit dem Programm:
Bei n = 58 und p = 0,37 ist P(20 ≤ X ≤ 25) = ? Lösung 3.
Beispiel 1: Eine Urne enthält 100 Kugeln, 30 rote und 70 blaue. Mit welcher Wahrscheinlichkeit erhält man bei 10 mal Ziehen 3 rote?
Bei Ziehen ohne Zurücklegen erhielte man P(X = 3) = 0,281163 . Bei Ziehen mit Zurücklegen ergibt die Binomialverteilung mit p = 0,3 und n = 10 die Wahrscheinlichkeit P(X = 3) = 0,266828 .
Nun enthält die Urne 1000 Kugeln, 300 rote und 700 blaue. Wir ziehen wieder 10 mal und wollen 3 rote Kugeln haben.
Bei Ziehen ohne Zurücklegen wäre P(X = 3) = 0,268171 . Bei Ziehen mit Zurücklegen ergibt die Binomialverteilung mit p = 0,3 und n = 10 wieder P(X = 3) = 0,266828 .
Da 300 und 700 wesentlich größer sind als n = 10, unterscheiden sich die Ergebnisse mit und ohne Zurücklegen relativ wenig. Daher rechnet man auch beim Ziehen ohne Zurücklegen, z.B. bei einer Meinungsumfrage, mit der einfacheren Binomialverteilung. (Eigentlich müßte man die hypergeometrische Verteilung nehmen.) Die Angabe der Werte auf sechs Stellen ist meist nicht sinnvoll.
Beispiel 2: In den Teig von 100 Brötchen werden 1000 Rosinen gemischt. Mit welcher Wahrscheinlichkeit enthält ein Brötchen 8-12 Rosinen?
Es werden n = 1000 Rosinen verteilt, und jede gelangt mit p = 1/100 = 0,01 in das eine Brötchen. Damit ist
P(8 ≤ X ≤ 12) = P(x ≤ 12) - P(X ≤ 7) = 0,792512 - 0,218863 = 0,573649 .
Beispiel 3: Die 120 Lehrerinnen und Lehrer einer Schule haben jeden Tag 60 Minuten Pause, von denen sie eine Minute mit Kopieren verbringen. Es sind zwei Kopierer vorhanden. Mit welcher Wahrscheinlichkeit muss zu einem Zeitpunkt niemand warten?
Es wird n = 120 mal zufällig entschieden, ob die betreffende Lehrperson in dieser Minute kopieren will. Die Wahrscheinlichkeit dafür ist p = 1/60 = 0,01666667 . Die Wahrscheinlichkeit dafür, dass zwei Kopierer ausreichen, ist P(X ≤ 2) = 0,676683 .
Aufgabe 1: Bei einer Meinungsumfrage gaben 80% der 10000 Befragten an, dass sie Statistiken misstrauen. Wenn wir das als repräsentativ ansehen, und nochmal 100 Leute befragen, mit welcher Wahrscheinlichkeit sind weniger als 70 davon misstrauisch? Lösung 1.
Aufgabe 2: In einer Stadt passieren im Jahr 700 Verkehrsunfälle. Mit welcher Wahrscheinlichkeit geschehen an einem bestimmten Tag mehr als 3 Unfälle? Lösung 2.
Aufgabe 3: Die 19 Schülerinnen und Schüler eines Kurses haben im Schnitt drei Fragen in einer Doppelstunde (90 Minuten), deren Beantwortung im Schnitt eine Minute dauert. Mit welcher Wahrscheinlichkeit müssen sie jeweils warten, weil der Lehrer bereits eine andere Frage beantwortet? Lösung 3.
μ = 0*P(X = 0) + 1*P(X = 1) + 2*P(X = 2) + ... +n*P(X = n) ,
und zur Berechnung verwende die einfache Formel μ = pn.
Im Histogramm der Binomialverteilung ist der Erwartungswert als höchster Punkt zu erkennen, denn das Maximum von P(X = k) liegt bei μ - q ≤ k ≤ μ + p. Das Programm zeigt den Wert von μ in der oberen Zeile an. Als Hintergrund des Histogramms zeigt es sieben graue Striche, der mittlere ist bei μ.
Aufgabe 1: Setze n = 100 und p = 0,1. Erhöhe p schrittweise zu 0,2 , 0,3 ... , beobachte wie sich das Histogramm verändert.
Die Standardabweichung σ kannst Du mit der Formel σ = √pqn berechnen. Ein größerer Wert von σ bedeutet, dass die Werte von X wahrscheinlich stärker vom Erwartungswert μ abweichen. Das Histogramm ist breiter und flacher. Das Programm zeigt den Wert von σ in der oberen Zeile an. Die grauen Striche haben den Abstand σ.
Da σ zu √n proportional ist, ergibt sich für großen Stichprobenumfang n folgendes: Die Standardabweichung σ wächst auch, aber langsamer als n. Wenn man z.B. n vervierfacht, wird σ nur verdoppelt. Im Verhältnis zu n wird σ klein, d.h. das Histogramm wird spitzer. Die wahrscheinlichen Werte von X weichen relativ gesehen weniger vom Erwartungswert μ ab.
Aufgabe 2: Setze n = 100 und p = 0,3. Erhöhe n schrittweise zu 200, 300 ... , beobachte wie sich das Histogramm verändert.
Beispiel 1: Theoretisch sollte ungefähr P(X ≤ μ + σ) ≈ 0,841 und P(X ≤ μ + 1,64σ) ≈ 0,95 gelten.
Aufgabe 1: Überprüfe dies für p = 0,3 und n = 100, n = 500, n = 1000.
Die Variable z zählt die Abweichung von μ in Einheiten von σ, also k = μ + σz. Die Wahrscheinlichkeit P(X ≤ k) hängt näherungsweise nur von z ab. Das Programm zeigt k und z in der Statuszeile an, wenn du die Maus bewegst.
Aufgabe 2: Überprüfe, dass die senkrechten Striche den Abstand σ haben, und dass k um σ wächst, wenn z um 1 größer wird.
Aufgabe 1: Variiere p und n, nachdem Du F3 gedrückt hast. Probiere alle Kombinationen von F2, F3, F4 aus.
Die kumulierte Bimomialverteilung P(X ≤ k) ist der Flächeninhalt des Histogramms bis zur Stelle k + 0,5. Die Integralfunktion Φ(z) zu φ(z) wird zur näherungsweisen Berechnung der kumulierten Bimomialverteilung verwendet. Dazu wird die Gleichung k + 0,5 = μ + σz nach z aufgelöst, also z = (k + 0,5 – μ)/σ , und es gilt P(X ≤ k) ≈ Φ(z) .
Aufgabe 2: Probiere dies für verschiedene Werte von n, p, k aus: Berechne einmal P(X ≤ k) mit dem Programm (Taste x). Berechne dann μ, σ, z und schließlich Φ(z), entweder mit einer Tabelle oder mit dem Programm (Taste z).
Der Sinn der Näherungsformel ist zum einen der, dass man statt drei Variablen n, p, k nur noch die eine Variable z hat, und somit nur noch eine Tabelle für alle möglichen Werte braucht. Zum anderen kann man z.B. Verwerfungsbereiche einfacher berechnen, etwa P(X ≤ μ - 1,64σ) ≈ 0,05 .
Für n = 100 und p = 1/6 gilt P(X ≤ 10) ≈ 5%. Daher legt man hier zum Signifikanzniveau α = 5% den linksseitigen Verwerfungsbereich 0 ≤ X ≤ 10 fest. Das bedeutet:
1) Wenn bei 100 mal Würfeln die Sechs X ≤ 10 mal fällt, sagen wir, dass das Ergebnis signifikant abweicht. Mit der Irrtumswahrscheinlichkeit α = 5% ist die Hypothese p = 1/6 widerlegt und p < 1/6.
2) Wenn bei 100 mal Würfeln die Sechs X > 10 mal fällt, weicht das Ergebnis nicht signifikant ab. Die Hypothese p = 1/6 wurde nicht widerlegt, kann aber trotzdem falsch sein.
Beachte, dass die Irrtumswahrscheinlichkeit von 5% im 1. Fall folgendes bedeutet:
Wenn die Hypothese p = 1/6 richtig ist, lehnen wir sie mit 5% Wahrscheinlichkeit irrtümlich ab, weil zufällig ein kleines Ergebnis auftritt.
Das bedeutet nicht:
Wenn wir die Hypothese aufgrund eines kleinen Stichprobenergebnisses ablehnen, ist sie mit 5% Wahrscheinlichkeit doch richtig. Dazu kann man keine Aussage machen!
Zur Bestimmung des Verwerfungsbereichs geht man so vor: Formuliere zunächst die Hypothese H1 , die Du bestätigen willst, hier H1: p < 1/6. Das Gegenteil ist die zu testende Nullhypothese H0 , hier H0: p = 1/6 oder p ≥ 1/6. Dann bestimme den Verwerfungsbereich:
1) Suche in der Tabelle das k so, dass P(X ≤ k) gerade ≤ 0,05 ist.
2) Oder drücke im Programm Binomial die Taste s und gib 0,05 ein.
3) Oder benutze die Näherungsformel k ≈ μ - 1,64σ.
Aufgabe 1: Partei A hatte bei der letzten Wahl 40%. Jetzt sagen bei einer Umfrage 30 von 100 Leuten, dass sie A wählen würden. Ist die Quote gesunken? Lösung 1.
Aufgabe 2: Partei B hatte bei der letzten Wahl 40%. Jetzt sagen bei einer Umfrage 45 von 100 Leuten, dass sie B wählen würden. Ist die Quote gestiegen? Lösung 2.
Die Irrtumswahrscheinlichkeit oder das Signifikanzniveau α ist die Wahrscheinlichkeit für den Fehler 1. Art, eine richtige Hypothese H0 irrtümlich zu verwerfen. β ist die Wahrscheinlichkeit für den Fehler 2. Art, dass eine falsche Hypothese H0 nicht verworfen wird, weil das Stichprobenergebnis zufällig nicht weit genug abweicht. Diese Wahrscheinlichkeit läßt sich nur abschätzen, wenn man eine mehr oder weniger willkürliche Annahme über die tatsächliche Wahrscheinlichkeit p trifft.
Beispiel 2: Gemäß Beispiel 1 halten wir den Würfel für unfair, wenn bei 100 mal Würfeln nur X ≤ 10 mal eine Sechs fällt. Angenommen, es ist tatsächlich nur p = 1/12. Dann ist β = P(X > 10) = 0,2106 die Wahrscheinlichkeit dafür, dass wir den Würfel nicht als unfair erkennen.
Aufgabe 3: Die Quote von Partei C ist tatsächlich von 40% auf 30% gesunken. Mit welcher Wahrscheinlichkeit weicht das Ergebnis einer Umfrage von 100 Leuten nicht signifikant von 40% ab? Lösung 3.
Beim zweiseitigen Hypothesentest will man z.B. die Hypothese H1: p ≠ 1/6 bestätigen, indem man die Nullhypothese H0: p = 1/6 widerlegt. Meines Erachtens ist dies bei α = 5% der Fall, wenn X ≤ 10 oder X ≥ 24 herauskommt. In Schulbüchern wird üblicherweise die Irrtumswahrscheinlichkeit halbiert: Jeder der einseitigen Verwerfungsbereiche soll eine Wahrscheinlichkeit von 2,5% haben, so dass H0 nur verworfen wird, wenn X ≤ 9 oder X ≥ 25 herauskommt.
Seite 1: Binomialverteilung
Beispiel 1: Es wird zehnmal gewürfelt, mit welcher Wahrscheinlichkeit fällt dreimal die Sechs?Es gibt (103) = 120 Möglichkeiten, an welcher Stelle eine Sechs auftritt (Pfade im Baumdiagramm), und jeweils die Pfadwahrscheinlichkeit (1/6)3*(5/6)7 = 0,001292045 , also ist die Wahrscheinlichkeit 120 * 0,001292045 = 0,155045 .
Binomialverteilung: Allgemein betrachten wir einen n-stufigen Versuch, wobei auf jeder Stufe der "Erfolg" mit derselben Wahrscheinlichkeit p eintritt. Die Wahrscheinlichkeit, dass die Anzahl X der Erfolge einen Wert k hat, ist dann P(X = k) = (nk)pkqn-k mit q = 1 - p . Der Binomialkoeffizient (nk) läßt sich z.B. mit dem Pascalschen Dreieck berechnen, oder auf vielen Taschenrechnern mit der Taste "nCr".
Das Programm Binomial zeigt die Binomialverteilung durch ein Histogramm an. Mit den Tasten p und n kannst Du die Erfolgswahrscheinlichkeit p und den Stichprobenumfang n verändern. Mit der Taste x kannst Du einen Wert für k eingegeben und die Wahrscheinlichkeit P(X = k) berechnen.
Die kumulierte Wahrscheinlichkeit ist die Wahrscheinlichkeit für höchstens k Erfolge,
P(X ≤ k) = P(X = 0) + P(X = 1) + ... + P(X = k) .
Das Programm berechnet mit der Taste x auch die kumulierte Wahrscheinlichkeit. Für spezielle Werte von p und n gibt es auch Tabellen, und eine allgemeine Näherungsformel wird auf Seite 5 vorgestellt. Die Berechnung mit dem Taschenrechner wäre für große k sehr mühsam. Mit der Taste F2 wird die kumulierte Verteilung als Diagramm dargestellt, und zwar als Integralfunktion des Histogramms. Jeweils der rechte Rand eines Trapezes gibt eine kumulierte Wahrscheinlichkeit an.
Beispiel 2: Für n = 100 und p = 0,4 ergibt sich die Wahrscheinlichkeit für mindestens 30 und höchstens 40 Erfolge,
P(30 ≤ X ≤ 40) = P(X ≤ 40) - P(X ≤ 29) = 0,543294 - 0,014775 = 0,528519 .
Aufgabe 1: Berechne die Wahrscheinlichkeit mit dem Taschenrechner und mit dem Programm:
Bei n = 37 und p = 0,58 ist P(X = 25) = ? Lösung 1.
Aufgabe 2: Bestimme die kumulierte Wahrscheinlichkeit mit einer Tabelle und mit dem Programm:
Bei n = 50 und p = 1/6 = 0,16666667 ist P(X ≥ 10) = ? Lösung 2.
Aufgabe 3: Berechne die kumulierte Wahrscheinlichkeit mit dem Programm:
Bei n = 58 und p = 0,37 ist P(20 ≤ X ≤ 25) = ? Lösung 3.
Seite 2: Anwendungen
Einige typische Anwendungen der Binomialverteilung, die sich mit dem Programm berechnen lassen, z.T. auch mit Tabellen oder dem Taschenrechner:Beispiel 1: Eine Urne enthält 100 Kugeln, 30 rote und 70 blaue. Mit welcher Wahrscheinlichkeit erhält man bei 10 mal Ziehen 3 rote?
Bei Ziehen ohne Zurücklegen erhielte man P(X = 3) = 0,281163 . Bei Ziehen mit Zurücklegen ergibt die Binomialverteilung mit p = 0,3 und n = 10 die Wahrscheinlichkeit P(X = 3) = 0,266828 .
Nun enthält die Urne 1000 Kugeln, 300 rote und 700 blaue. Wir ziehen wieder 10 mal und wollen 3 rote Kugeln haben.
Bei Ziehen ohne Zurücklegen wäre P(X = 3) = 0,268171 . Bei Ziehen mit Zurücklegen ergibt die Binomialverteilung mit p = 0,3 und n = 10 wieder P(X = 3) = 0,266828 .
Da 300 und 700 wesentlich größer sind als n = 10, unterscheiden sich die Ergebnisse mit und ohne Zurücklegen relativ wenig. Daher rechnet man auch beim Ziehen ohne Zurücklegen, z.B. bei einer Meinungsumfrage, mit der einfacheren Binomialverteilung. (Eigentlich müßte man die hypergeometrische Verteilung nehmen.) Die Angabe der Werte auf sechs Stellen ist meist nicht sinnvoll.
Beispiel 2: In den Teig von 100 Brötchen werden 1000 Rosinen gemischt. Mit welcher Wahrscheinlichkeit enthält ein Brötchen 8-12 Rosinen?
Es werden n = 1000 Rosinen verteilt, und jede gelangt mit p = 1/100 = 0,01 in das eine Brötchen. Damit ist
P(8 ≤ X ≤ 12) = P(x ≤ 12) - P(X ≤ 7) = 0,792512 - 0,218863 = 0,573649 .
Beispiel 3: Die 120 Lehrerinnen und Lehrer einer Schule haben jeden Tag 60 Minuten Pause, von denen sie eine Minute mit Kopieren verbringen. Es sind zwei Kopierer vorhanden. Mit welcher Wahrscheinlichkeit muss zu einem Zeitpunkt niemand warten?
Es wird n = 120 mal zufällig entschieden, ob die betreffende Lehrperson in dieser Minute kopieren will. Die Wahrscheinlichkeit dafür ist p = 1/60 = 0,01666667 . Die Wahrscheinlichkeit dafür, dass zwei Kopierer ausreichen, ist P(X ≤ 2) = 0,676683 .
Aufgabe 1: Bei einer Meinungsumfrage gaben 80% der 10000 Befragten an, dass sie Statistiken misstrauen. Wenn wir das als repräsentativ ansehen, und nochmal 100 Leute befragen, mit welcher Wahrscheinlichkeit sind weniger als 70 davon misstrauisch? Lösung 1.
Aufgabe 2: In einer Stadt passieren im Jahr 700 Verkehrsunfälle. Mit welcher Wahrscheinlichkeit geschehen an einem bestimmten Tag mehr als 3 Unfälle? Lösung 2.
Aufgabe 3: Die 19 Schülerinnen und Schüler eines Kurses haben im Schnitt drei Fragen in einer Doppelstunde (90 Minuten), deren Beantwortung im Schnitt eine Minute dauert. Mit welcher Wahrscheinlichkeit müssen sie jeweils warten, weil der Lehrer bereits eine andere Frage beantwortet? Lösung 3.
Seite 3: μ und σ
Der Erwartungswert μ ist der ideale Mittelwert der Erfolgszahl X: Wenn man das n-stufige Zufallsexperiment sehr oft wiederholt, erhält man im Durchschnitt μ Erfolge. Er ist definiert alsμ = 0*P(X = 0) + 1*P(X = 1) + 2*P(X = 2) + ... +n*P(X = n) ,
und zur Berechnung verwende die einfache Formel μ = pn.
Im Histogramm der Binomialverteilung ist der Erwartungswert als höchster Punkt zu erkennen, denn das Maximum von P(X = k) liegt bei μ - q ≤ k ≤ μ + p. Das Programm zeigt den Wert von μ in der oberen Zeile an. Als Hintergrund des Histogramms zeigt es sieben graue Striche, der mittlere ist bei μ.
Aufgabe 1: Setze n = 100 und p = 0,1. Erhöhe p schrittweise zu 0,2 , 0,3 ... , beobachte wie sich das Histogramm verändert.
Die Standardabweichung σ kannst Du mit der Formel σ = √pqn berechnen. Ein größerer Wert von σ bedeutet, dass die Werte von X wahrscheinlich stärker vom Erwartungswert μ abweichen. Das Histogramm ist breiter und flacher. Das Programm zeigt den Wert von σ in der oberen Zeile an. Die grauen Striche haben den Abstand σ.
Da σ zu √n proportional ist, ergibt sich für großen Stichprobenumfang n folgendes: Die Standardabweichung σ wächst auch, aber langsamer als n. Wenn man z.B. n vervierfacht, wird σ nur verdoppelt. Im Verhältnis zu n wird σ klein, d.h. das Histogramm wird spitzer. Die wahrscheinlichen Werte von X weichen relativ gesehen weniger vom Erwartungswert μ ab.
Aufgabe 2: Setze n = 100 und p = 0,3. Erhöhe n schrittweise zu 200, 300 ... , beobachte wie sich das Histogramm verändert.
Seite 4: σ-Umgebungen
Die Standardabweichung σ gibt an, wie weit die wahrscheinlichen X-Werte vom Erwartungswert μ entfernt liegen. Deshalb kann man die Wahrscheinlichkeit P(X ≤ k) näherungsweise berechnen, wenn man weiß, um wie viele σ das k von μ entfernt ist.Beispiel 1: Theoretisch sollte ungefähr P(X ≤ μ + σ) ≈ 0,841 und P(X ≤ μ + 1,64σ) ≈ 0,95 gelten.
Aufgabe 1: Überprüfe dies für p = 0,3 und n = 100, n = 500, n = 1000.
Die Variable z zählt die Abweichung von μ in Einheiten von σ, also k = μ + σz. Die Wahrscheinlichkeit P(X ≤ k) hängt näherungsweise nur von z ab. Das Programm zeigt k und z in der Statuszeile an, wenn du die Maus bewegst.
Aufgabe 2: Überprüfe, dass die senkrechten Striche den Abstand σ haben, und dass k um σ wächst, wenn z um 1 größer wird.
Seite 5: Näherungsformeln
Mit der Taste F3 wird das Histogramm umskaliert dargestellt, so dass die x-Achse von μ - 3σ bis μ + 3σ geht, also z von –3 bis 3. Die y-Achse ist auch um den Faktor σ umskaliert. Es zeigt sich, dass sich das Histogramm in dieser Darstellung kaum verändert, wenn man p und n ändert. Mit F4 erhältst Du zum Vergleich die Kurve der Gaußschen Normalverteilung φ(z) = e-z2/2 / √2π .Aufgabe 1: Variiere p und n, nachdem Du F3 gedrückt hast. Probiere alle Kombinationen von F2, F3, F4 aus.
Die kumulierte Bimomialverteilung P(X ≤ k) ist der Flächeninhalt des Histogramms bis zur Stelle k + 0,5. Die Integralfunktion Φ(z) zu φ(z) wird zur näherungsweisen Berechnung der kumulierten Bimomialverteilung verwendet. Dazu wird die Gleichung k + 0,5 = μ + σz nach z aufgelöst, also z = (k + 0,5 – μ)/σ , und es gilt P(X ≤ k) ≈ Φ(z) .
Aufgabe 2: Probiere dies für verschiedene Werte von n, p, k aus: Berechne einmal P(X ≤ k) mit dem Programm (Taste x). Berechne dann μ, σ, z und schließlich Φ(z), entweder mit einer Tabelle oder mit dem Programm (Taste z).
Der Sinn der Näherungsformel ist zum einen der, dass man statt drei Variablen n, p, k nur noch die eine Variable z hat, und somit nur noch eine Tabelle für alle möglichen Werte braucht. Zum anderen kann man z.B. Verwerfungsbereiche einfacher berechnen, etwa P(X ≤ μ - 1,64σ) ≈ 0,05 .
Seite 6: Hypothesentest
Beispiel 1: Wenn man 100 mal würfelt, fällt die Sechs im Mittel 16,7 mal. Was bedeutet es, wenn sie 12 mal oder 8 mal fällt? Ist das eine zufällige Schwankung, oder weicht das Ergebnis signifikant von der Erwartung ab, d.h., der Würfel ist anscheinend gezinkt?Für n = 100 und p = 1/6 gilt P(X ≤ 10) ≈ 5%. Daher legt man hier zum Signifikanzniveau α = 5% den linksseitigen Verwerfungsbereich 0 ≤ X ≤ 10 fest. Das bedeutet:
1) Wenn bei 100 mal Würfeln die Sechs X ≤ 10 mal fällt, sagen wir, dass das Ergebnis signifikant abweicht. Mit der Irrtumswahrscheinlichkeit α = 5% ist die Hypothese p = 1/6 widerlegt und p < 1/6.
2) Wenn bei 100 mal Würfeln die Sechs X > 10 mal fällt, weicht das Ergebnis nicht signifikant ab. Die Hypothese p = 1/6 wurde nicht widerlegt, kann aber trotzdem falsch sein.
Beachte, dass die Irrtumswahrscheinlichkeit von 5% im 1. Fall folgendes bedeutet:
Wenn die Hypothese p = 1/6 richtig ist, lehnen wir sie mit 5% Wahrscheinlichkeit irrtümlich ab, weil zufällig ein kleines Ergebnis auftritt.
Das bedeutet nicht:
Wenn wir die Hypothese aufgrund eines kleinen Stichprobenergebnisses ablehnen, ist sie mit 5% Wahrscheinlichkeit doch richtig. Dazu kann man keine Aussage machen!
Zur Bestimmung des Verwerfungsbereichs geht man so vor: Formuliere zunächst die Hypothese H1 , die Du bestätigen willst, hier H1: p < 1/6. Das Gegenteil ist die zu testende Nullhypothese H0 , hier H0: p = 1/6 oder p ≥ 1/6. Dann bestimme den Verwerfungsbereich:
1) Suche in der Tabelle das k so, dass P(X ≤ k) gerade ≤ 0,05 ist.
2) Oder drücke im Programm Binomial die Taste s und gib 0,05 ein.
3) Oder benutze die Näherungsformel k ≈ μ - 1,64σ.
Aufgabe 1: Partei A hatte bei der letzten Wahl 40%. Jetzt sagen bei einer Umfrage 30 von 100 Leuten, dass sie A wählen würden. Ist die Quote gesunken? Lösung 1.
Aufgabe 2: Partei B hatte bei der letzten Wahl 40%. Jetzt sagen bei einer Umfrage 45 von 100 Leuten, dass sie B wählen würden. Ist die Quote gestiegen? Lösung 2.
Die Irrtumswahrscheinlichkeit oder das Signifikanzniveau α ist die Wahrscheinlichkeit für den Fehler 1. Art, eine richtige Hypothese H0 irrtümlich zu verwerfen. β ist die Wahrscheinlichkeit für den Fehler 2. Art, dass eine falsche Hypothese H0 nicht verworfen wird, weil das Stichprobenergebnis zufällig nicht weit genug abweicht. Diese Wahrscheinlichkeit läßt sich nur abschätzen, wenn man eine mehr oder weniger willkürliche Annahme über die tatsächliche Wahrscheinlichkeit p trifft.
Beispiel 2: Gemäß Beispiel 1 halten wir den Würfel für unfair, wenn bei 100 mal Würfeln nur X ≤ 10 mal eine Sechs fällt. Angenommen, es ist tatsächlich nur p = 1/12. Dann ist β = P(X > 10) = 0,2106 die Wahrscheinlichkeit dafür, dass wir den Würfel nicht als unfair erkennen.
Aufgabe 3: Die Quote von Partei C ist tatsächlich von 40% auf 30% gesunken. Mit welcher Wahrscheinlichkeit weicht das Ergebnis einer Umfrage von 100 Leuten nicht signifikant von 40% ab? Lösung 3.
Beim zweiseitigen Hypothesentest will man z.B. die Hypothese H1: p ≠ 1/6 bestätigen, indem man die Nullhypothese H0: p = 1/6 widerlegt. Meines Erachtens ist dies bei α = 5% der Fall, wenn X ≤ 10 oder X ≥ 24 herauskommt. In Schulbüchern wird üblicherweise die Irrtumswahrscheinlichkeit halbiert: Jeder der einseitigen Verwerfungsbereiche soll eine Wahrscheinlichkeit von 2,5% haben, so dass H0 nur verworfen wird, wenn X ≤ 9 oder X ≥ 25 herauskommt.